Panofskys Fluchtachsenprinzip in 3D CAD
Der erste Post mit Bildern heute. Ich mache mir zur Zeit Gedanken um die Ausführungen von Erwin Panowsky, die er um 1925 in Die Perspektive als symbolische Form veröffentlicht hat. Darin schreibt er einerseits, dass die Zentralperspektive keine genuine ›Erfindung‹ der Renaissance sei (wie etwa sehr gerne postuliert), sondern bereits in Vitruvs Ausführungen zur ›scenographia‹ in seinen Zehn Büchern über Architektur nachzuweisen sei.
Im Gegensatz zur ›modernen‹ Interpretation ist jedoch Vitruvs ›Centrum‹ (“omnium linearum ad circini centrum responsus”) nicht als einziger Fluchtpunkt anzusehen, sondern ahmt eher das natürliche menschliche Sehen nach.
Ich habe mir überlegt, wie sich diese Perspektive in 3D-CAD Software umsetzen lässt und wie das optische Resultat konkret aussieht. Dazu habe ich eine kleine Testszene gebastelt und gerendert:

Diese Szene hat gegenwärtig einen Fluchtpunkt (Zentralperspektive). Durch einen Multipass-Render mit mehreren Kameras habe ich versucht, die Multiperspektive, die Panofsky mit ›Fischgrät-‹ oder ›Fluchtachsenprinzip‹ (vgl. Panowsky 1980: 106) umschreibt, nachzuahmen.
Als ›quick-and-dirty‹-Setup sieht die 3D-Szene folgendermaßen aus:
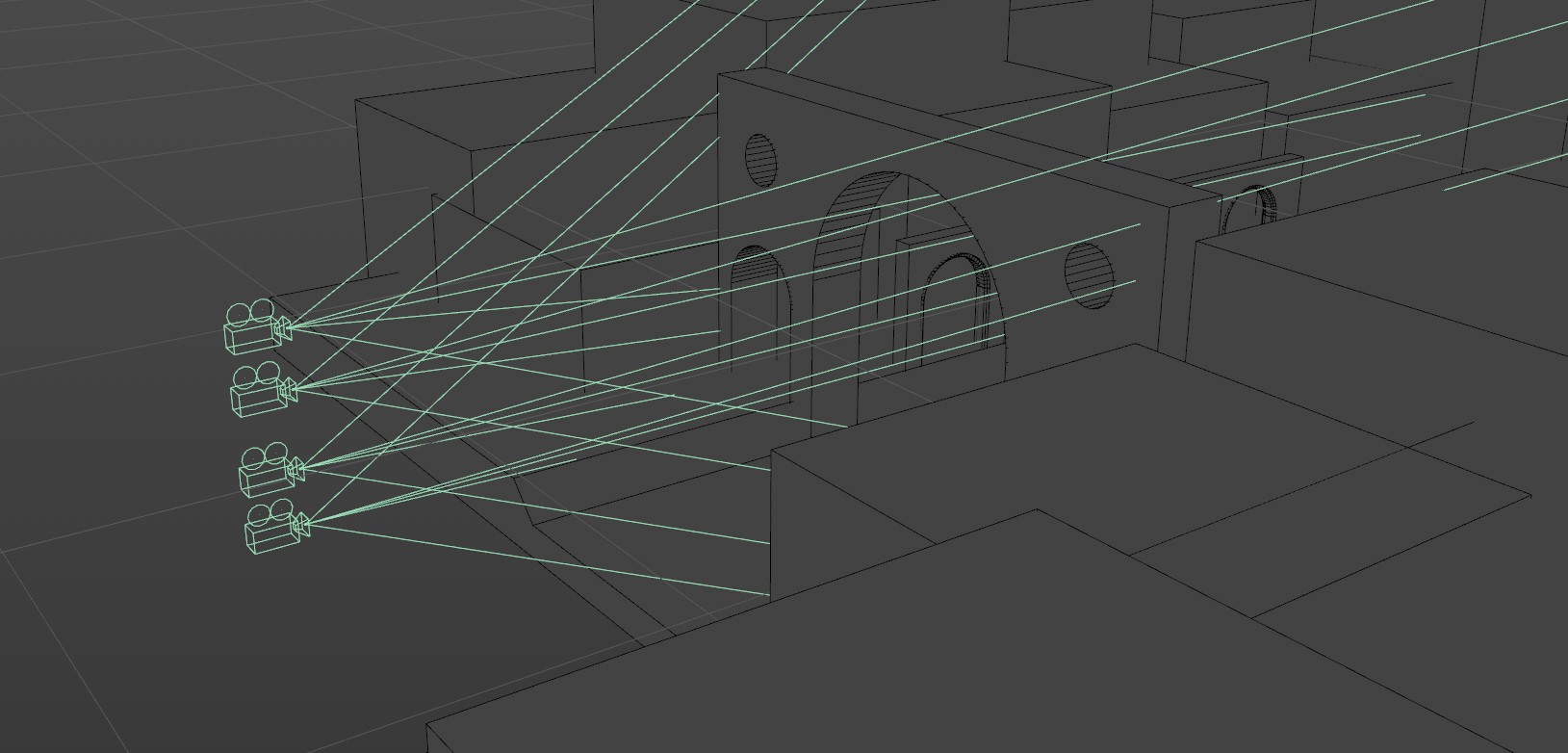
Der Versuch ist im Moment noch sehr beschränkt (die einzelnen Kameras unterscheiden sich ausschließlich durch ihre Position auf der Y-Achse (für alle Blender-Nutzer: Z-Achse)). Denkbar wäre etwa auch den Kippwinkel (›Elevation‹) der einzelnen Kameras zu iterieren, was ich in diesem ersten Versuch aber noch nicht umgesetzt habe.
Drei dieser Kameras habe ich in ihren jeweiligen Perspektiven gerendert und auf die Schnelle (!) in Photoshop kombiniert:

Auf den ersten Blick fällt nicht auf, dass die Fluchtpunkte nicht auf einen zentralen Punkt zusammenfallen. Erst wenn Linien gezeichnet werden, wird deutlich, dass das Rendering aus drei verschiedenen Fluchtpunkten besteht.

Panofskys ›Fischgräten‹ par excellence.
Update 1 (30. April 2021)
Habe in alten Dateien die folgende Skizze von mir gefunden, die Raffaels Schule von Athen in ihren jeweiligen Fluchtachsen untersucht. Die Idee dazu kam mir, weil ich damals Tobias Holischkas CyberPlaces – Philosophische Annäherungen an den virtuellen Ort gelesen habe, der die Multiperspektivität in dem Fresko ebenfalls anspricht. Problem dabei ist, dass die von mir angefertigte Skizze von falschen Voraussetzungen ausgeht – nämlich, dass der Torbogen Bestandteil des Gemäldes ist (was jedoch nicht der Fall ist). Trotzdem finden sich mehrere Perspektiven im Fresko selbst, konkret: Einerseits die Perspektive des Raumes (= der Architektur) und andererseits die Perspektive, mit der die einzelnen Menschen gemalt sind.
Um sie trotzdem nicht unter den Tisch fallen zu lassen, hier die falsche Skizze:
